vastdom.blogg.se - The optimal polynomial order sequential testing in r

THE OPTIMAL POLYNOMIAL ORDER SEQUENTIAL TESTING IN R SERIES

As we discuss further in Section 3, developing practical, simple tests for this pair of hypotheses is an active area of research (refs. A natural candidate is to base the test on the likelihood-ratio statistic but this turns out to have an intractable limiting distribution ( 3). Finding a test that provably controls the type I error at a given level has been elusive. Where M k denotes the set of mixtures of k Gaussians, with an appropriately restricted parameter space Θ (see for instance ref. Finally, when combined with the method of sieves, it can be used to perform model selection with nested model classes.

Further, the split LRT can be used with profile likelihoods to deal with nuisance parameters, and it can also be run sequentially to yield anytime-valid P values and confidence sequences. We investigate some conditions under which our methods yield valid inferences under model misspecification. We show that in settings when computing the MLE is hard, for the purpose of constructing valid tests and intervals, it is sufficient to upper bound the maximum likelihood. We also develop various extensions of our basic methods. Canonical examples arise in mixture modeling and shape-constrained inference, for which constructing tests and confidence sets has been notoriously difficult. The method we suggest works for any parametric model and also for some nonparametric models, as long as computing a maximum-likelihood estimator (MLE) is feasible under the null. Our method is especially appealing for statistical inference in these complex setups. The (limiting) null distribution of the classical likelihood-ratio statistic is often intractable when used to test composite null hypotheses in irregular statistical models. We refer to such procedures as “universal.” The method is very simple and is based on a modified version of the usual likelihood-ratio statistic that we call “the split likelihood-ratio test” (split LRT) statistic. 16.10 The Heckit, or Sample Selection ModelĪ multiple regression model is very similar to the simple regression model, but includes more independent variables.We propose a general method for constructing confidence sets and hypothesis tests that have finite-sample guarantees without regularity conditions.14 Time-Varying Volatility and ARCH Models.13.4 Impulse Responses and Variance Decompositions.12.1 AR(1), the First-Order Autoregressive Model.

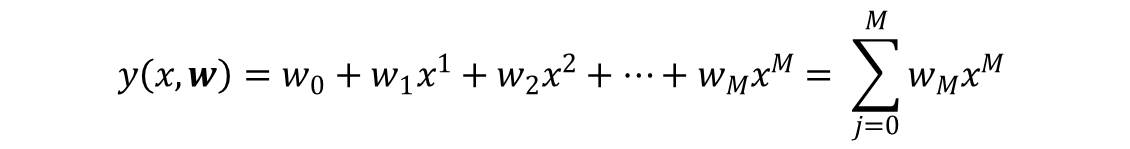
10.1 The Instrumental Variables (IV) Method.9.4 Estimation with Serially Correlated Errors.

THE OPTIMAL POLYNOMIAL ORDER SEQUENTIAL TESTING IN R SERIES

9.1 An Overview of Time Series Tools in R.

8.7 Heteroskedasticity in the Linear Probability Model.

8.3 Heteroskedasticity-Consistent Standard Errors.

8.1 Spotting Heteroskedasticity in Scatter Plots.

7.9.2 ggplot2, An Excellent Data Visualising Tool.

7.7 The Difference-in-Differences Estimator.

7.4 Indicator Variables in Log-Linear Models.

7.3 Comparing Two Regressions: the Chow Test.

6.1 Joint Hypotheses and the F-statistic.

6 Further Inference in Multiple Regression.

5.7 Goodness-of-Fit in Multiple Regression.

5.6 Interaction Terms in Linear Regression.

5.4 Hypothesis Testing in Multiple Regression.

5.3 Interval Estimation in Multiple Regression.

5.2 Example: Big Andy’s Hamburger Sales.

4.1 Forecasting (Predicting a Particular Value).

3.7 Testing Linear Combinations of Parameters.

3.4 Confidence Intervals in Repeated Samples.

3.3 Example: Confidence Intervals in the food Model.

3.1 The Estimated Distribution of Regression Coefficients.

3 Interval Estimation and Hypothesis Testing.

2.8 Using Indicator Variables in a Regression.

2.6 Estimated Variances and Covariance of Regression Coefficients.

2.5 Repeated Samples to Assess Regression Coefficients.

2.4 Prediction with the Linear Regression Model.

2.2 Example: Food Expenditure versus Income.